八省联考的第十一题近些天引起热议。借此机会，我们来浅聊一下纽结理论(knot theory)。

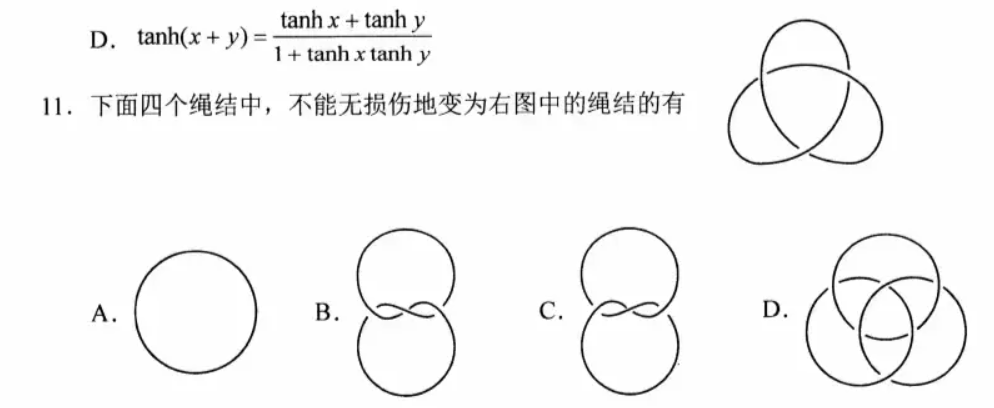
相信你小时候肯定也想过与这道题类似的问题：画出一个结的形状，怎么判定它是一个活结？也就是说，拉这个结的两端，最后能还原成一直线？

这是最早的，研究扭结理论的一个动机。但数学家又发现，如果有两个开放端的话，描述问题不够简便。所以他们规定，数学里的结是把两个开放端连起来的。这样数学里的“结”就是一条封闭的绳环，在三维空间里缠绕构成的一个空间多边形。

那么可以想象，一个绳环所能构成的最简单形状当然就是一个圆环。这是最简单的一种结，这种形状被称为“unknot”，中文叫“平凡结”。

一个游戏工作室Treyarch的logo，很像三叶结，但仔细观察会发现其实是平凡结

给定两个结，怎么判定它们其实是同一种结？对这么简单的结，我们可以目测判定。但是对更复杂的形状，目测就会失效，所以数学家希望找到合适的数学方法去研究扭结。

问题是，同一个扭结，形状可以千变万化。我们需要忽略绝大多数变化，只关注我们需要的变化。所以，数学家需要寻找的是“不变量”，也就是变化对象的某个不变的属性。就像我们再次见到几十年没见到的朋友，也许他的外貌变化很大，但是你可能发现，他的声音，神态，举止没有变化。那么这些属性就是“不变量”，这些属性可以帮我们识别一个人。

对一个扭结来说，有哪些不变量？你能想到的第一个属性应该是交叉点数。把一个扭结平放在桌上，通过整理，可以把绳与绳之间的交叉点减少若干。到一定程度后，就无法继续减少了。此时的交叉点数就是一个结的不变量。


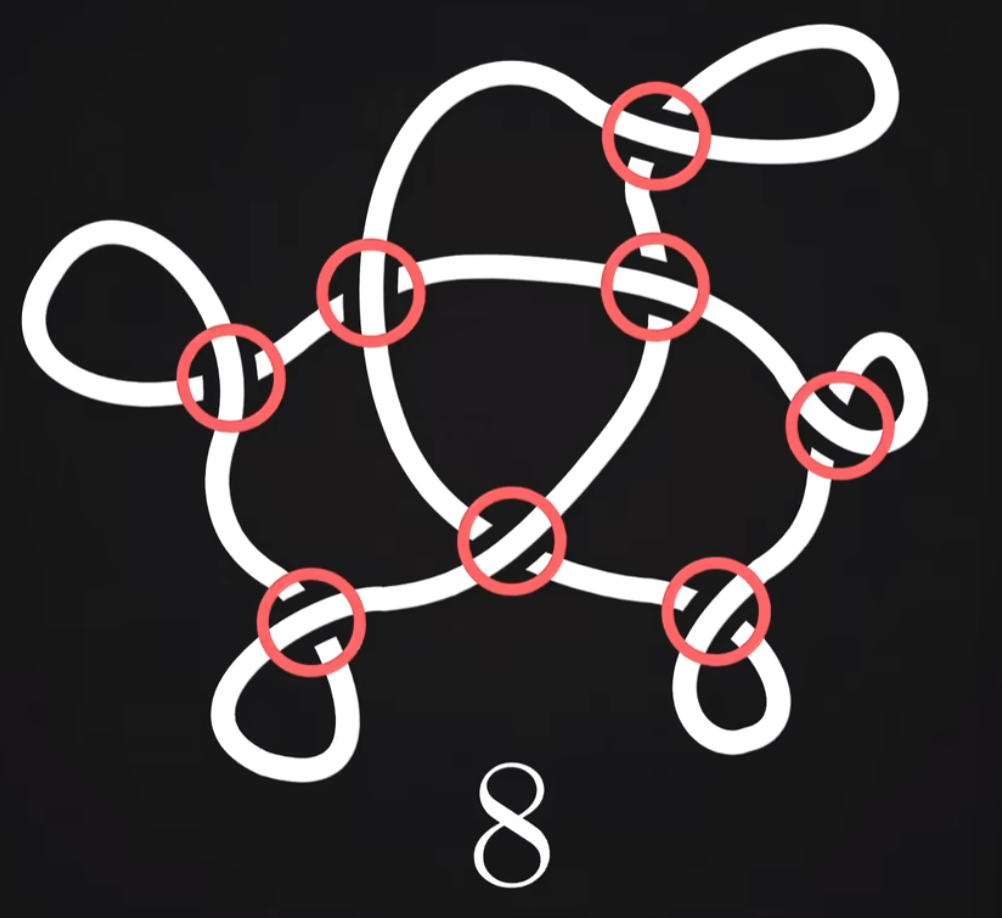
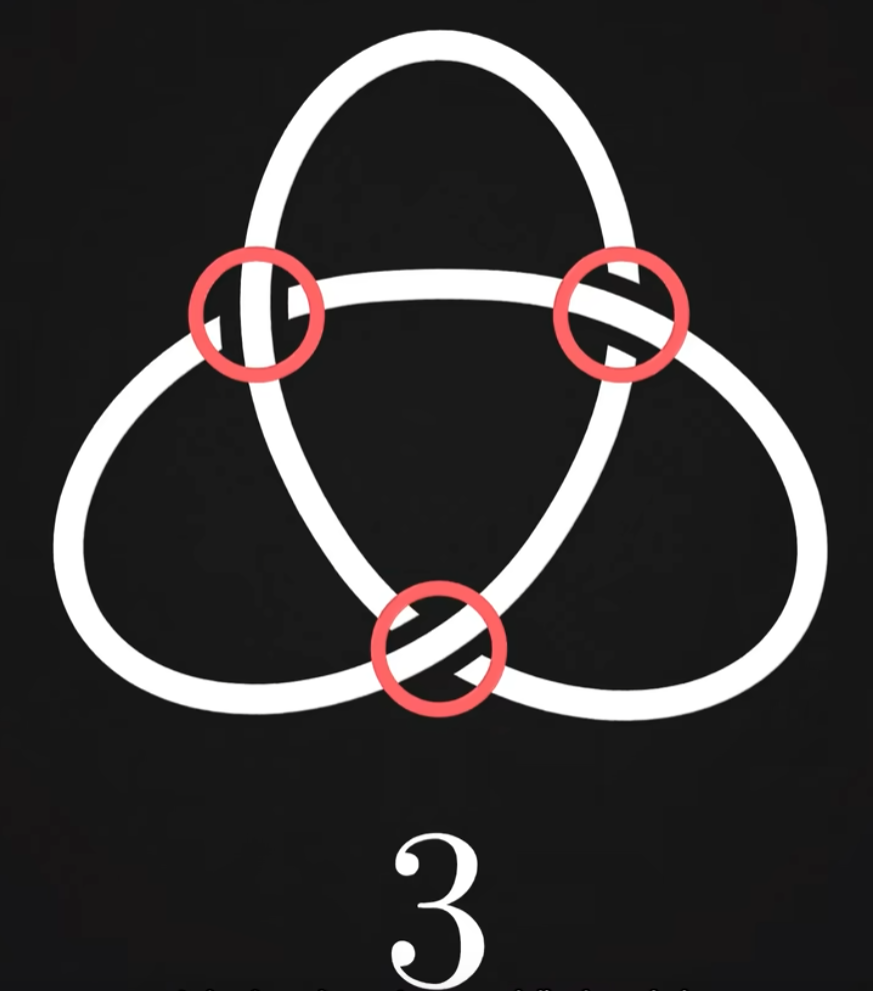
通过扭转之后可以发现交叉点最小为3

但可惜的是，交叉点数并不是一个很有用的扭结不变量，有两个原因：首先，给定一个结的形状，如何判定这个形状里的交叉点数最小？这并没有一个很好的方法。还有一个缺陷是，相同的交叉点数下，存在很多不同的扭结，而且交叉点越多，不同的扭结也越多。这也意味着交叉点数并不能很好的区分扭结。

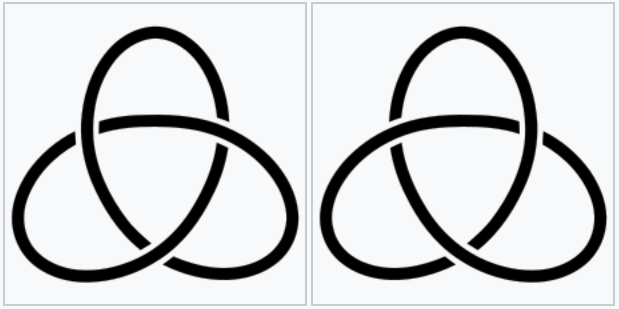
左手三叶结和右手三叶结。它们的交叉点数相同，但却是不同的结

所以目前数学家们使用更有用的不变量来判断扭结是否相等：扭结多项式。1928年，美国数学瓦德尔·亚历山大提出了一个扭结不变量，称为“亚历山大多项式”。并且他证明了，如果两个结可以互相转化，那么它们的这个特征多项式就可以互相转化。这样判定两个结是否等价就很容易了，因为判断多项式能否相互转换要比看图形方便多了。

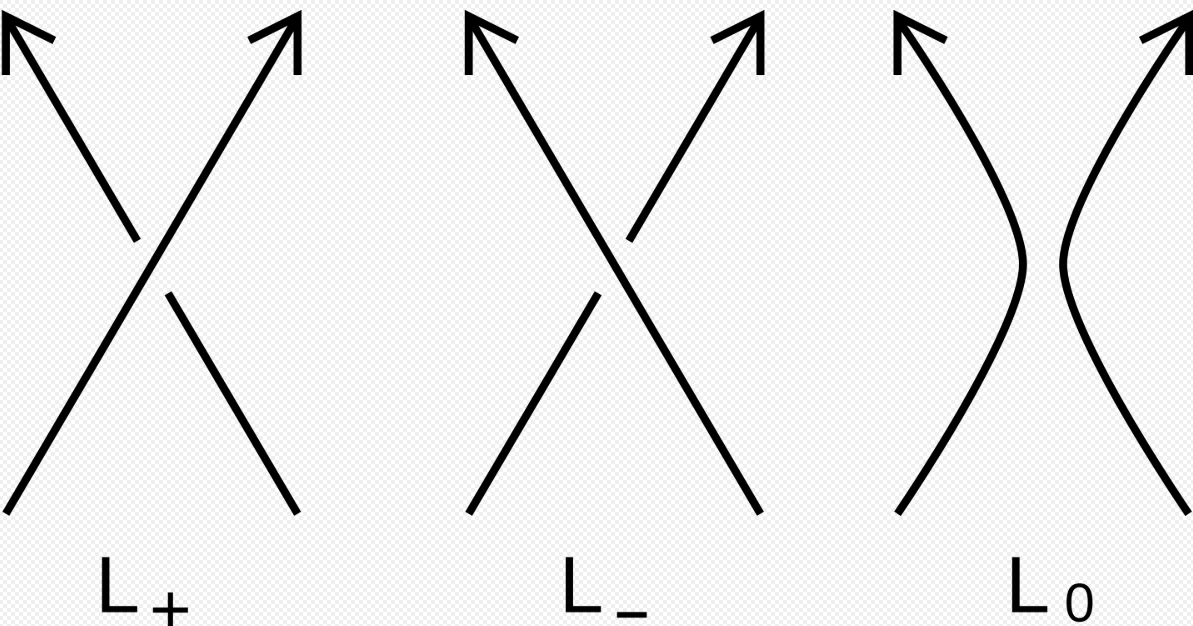
亚历山大多项式的规则相当简单：
$$
\nabla (O) = 1 \\
\nabla (L_+)-\nabla(L_-)=z\nabla(L_0)
$$
以平凡链环(unlink)为例：

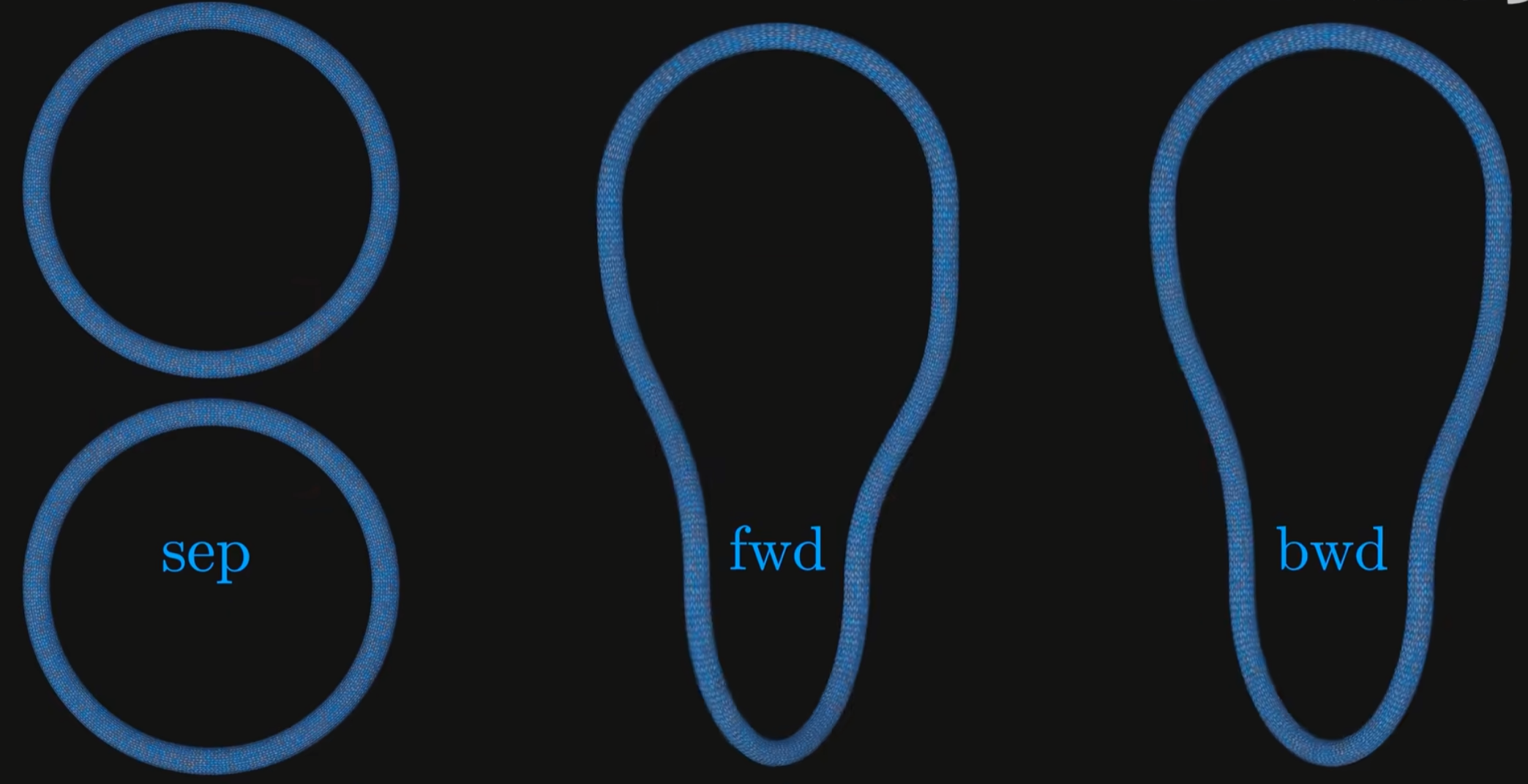
经历L+和L-变换后，均形成平凡结；而平凡结的亚历山大多项式定义为1，故平凡链环的多项式为
$$
1-1=z\nabla(Unlink) \\
\nabla(Unlink)=0
$$
但是亚历山大多项式也有一个明显的的缺陷：少数情况下，不同的结仍然会具有相同的亚历山大多项式，特别是一个结和它的镜像，必然有相同的亚历山大多项式。显然一个结和它的镜像在变换的意义上是相同的，但你无论怎么变换也没办法吧一个结变成它的镜像。所以，从这个意义上说，一个结和它的镜像是两种结，但是亚历山大多项式是无法区分它们的。

扭结理论的再一次重大突破是在1984年。新西兰数学家沃恩·琼斯发现了另一个扭结不变量，称为“琼斯多项式”。这个多项式在区分和表达扭结的能力上比“亚历山大多项”式强许多。

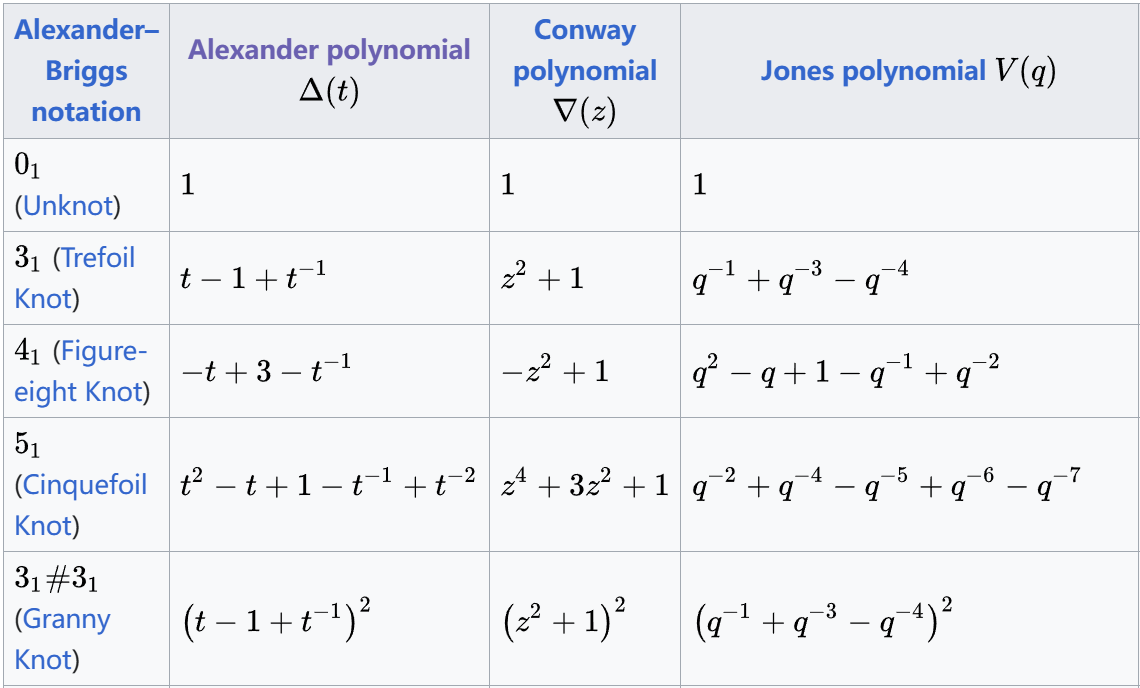
一些结的亚历山大多项式和琼斯多项式。可以发现琼斯多项式能更好地区分扭结。

更为奇妙的是，在琼斯发表了琼斯多项式之后不久，美国物理学家爱德华·威腾发现了琼斯多项式与量子场论之间有着奇妙的联系。爱德华·威腾是弦理论和量子场论的顶尖专家，并且是“M理论”的创立者。而M理论是目前一种比较有希望的“大统一理论”。爱德华·威腾发现琼斯多项式可以运用到量子场论里，这个发现让人遐想连篇：难道宇宙的微观结构中存在一个个扭结？

不管怎样，琼斯和威腾的发现是如此重要，使得二人在1990年，获得了数学界的最高荣誉之一：菲尔兹奖。那次菲尔茨奖有两个不寻常之处，一个是威腾是目前仅有的获得菲尔兹奖的物理学家；琼斯则被认为是以最短的论文获得菲尔兹奖的人。琼斯的关于琼斯多项式的论文一共8页，其中有4页是一些数据表格和引用之类，论文实际内容只有4页。仅凭4页的论文获得菲尔兹奖，这也是绝无仅有的例子。

下面再简单聊聊扭结的另外一种有趣的性质：扭结的分解和加法组合。

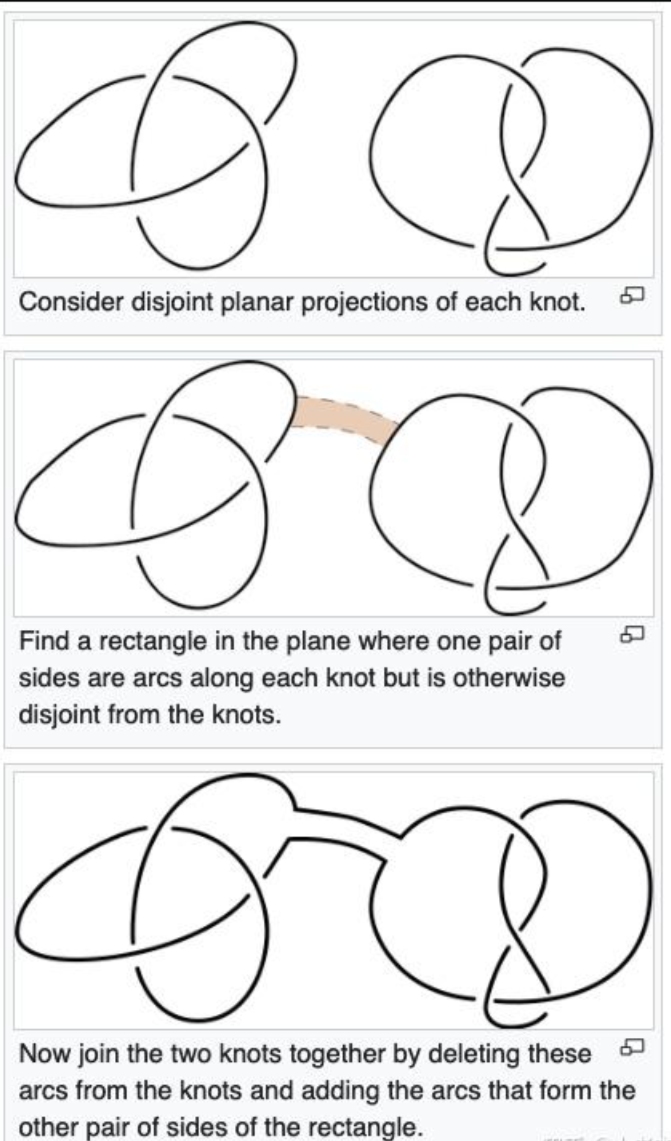
结的“加法”：把两个结尽量放平在桌面上，互不重合。在两个结之间，找某个比较靠近的部分，画一个矩形。要求矩形两对边分别在两个结上，不覆盖任何结。在矩形两对边处，各剪一刀，得到4个开放端，上面的两个开放端连在一起，下面的两个开放端连在一起，就得到了一个新的结。在严格的定义下，这种加法的结果是唯一的。

结的加法有了，那么它的逆操作就是结的分解。有了组合和分解操作后，一下子就可以考虑很多有意思的问题。结的加法有没有交换律和结合律？答案是肯定的，你可以试着验证一下。

还有一个“显然”的结论是：一个结加上平凡结，所得结果是其本身。那么是否存在两个或多个非平凡结，它们相加后变为平凡结呢？可能有人会有这种想法：一个结加上它镜子里的图像，两者就会互相“抵消”，最后变成一个平凡结。但答案有点意外，是否定的。1949年，数学家舒伯特证明了：一个非平凡结，无论给它加上怎样的结，也没法“抵消”它，最后变成一个平凡结。

再看看结的分解，就更有意思了。结的分解就是结加法的逆运算。显然，存在这样一些结，对它们没法分解了。如果继续分解，也只能分出平凡结，比如三叶结。那么对这种没法分解的解，数学家给它起了个名字（也许你猜到了）：“素结”（Prime Knot）。

这就马上带来一个有意思的问题：结的世界中，有“唯一因子分解定理”吗？也就是，当一个结不是素结，而是一个“合结”的时候，把这个“合结”分解为若干素结的组合，那么分解结果是唯一的吗？

答案是肯定的，1949年，还是数学家舒伯特证明了：把结的方向定向之后，合结的分解结果是唯一的。

那有没有一个办法判定一个结是素结呢？答案如同质因数分解，目前没有一个简单的方法或者快捷算法，判定一个结是否是素结，或者分解一个合结。所以，给定一个结，如何对其“素结分解”也就是一个比较困难的问题。由此，甚至有人设想，参考RSA算法的动机，可以用“结”，构造一个非对称加密体系。

扭结理论作为数学、物理学、化学和生物学等多个学科的交汇点，为这些领域之间提供了共同的语言和工具。理解纽结理论，将有助于我们把这些理论联系起来。