线性代数(一)
本章的主要内容有:
- 线性方程组的解
- 系数矩阵与增广矩阵
- 向量方程组
线性方程组
包含变量$x_1,x_2,…,x_n$的线性方程是形如
$$ a_1x_1+a_2x_2+…+a_nx_n=b$$
的方程,其中$b$与系数$a_1,a_2,…a_n$是实数或负数,下标$n$可以是任意正整数。
方程
$$ 4x_1-5x_2=x_1x_2 和 x_2=2\sqrt{x_1}-6$$
都不是线性方程,因为第一个方程中包含$x_1x_2$,而第二个方程中包含$\sqrt{x_1}$.
线性方程组是由一个或几个包含相同变量$x_1,x_2,…,x_n$的线性方程组成的. 例如,
$$ \begin{align*}
2x_1 - x_2 + 1.5x_3 &= 8 \\
x_1 \phantom{1.-x_2} - 4x_3 &= -7
\end{align*}$$
线性方程组的解是一组数$(s_1,s_2,..s_n)$, 用这组数代入$x_1,x_2,…,x_n$时所有方程均成立.
方程组所有可能解的集合称为线性方程组的解集. 若两个线性方程组解集相同,我们称这两个线性方程组为等价的. 也就是说,第一个方程组的每个解都是第二个方程组的解,反之亦然。
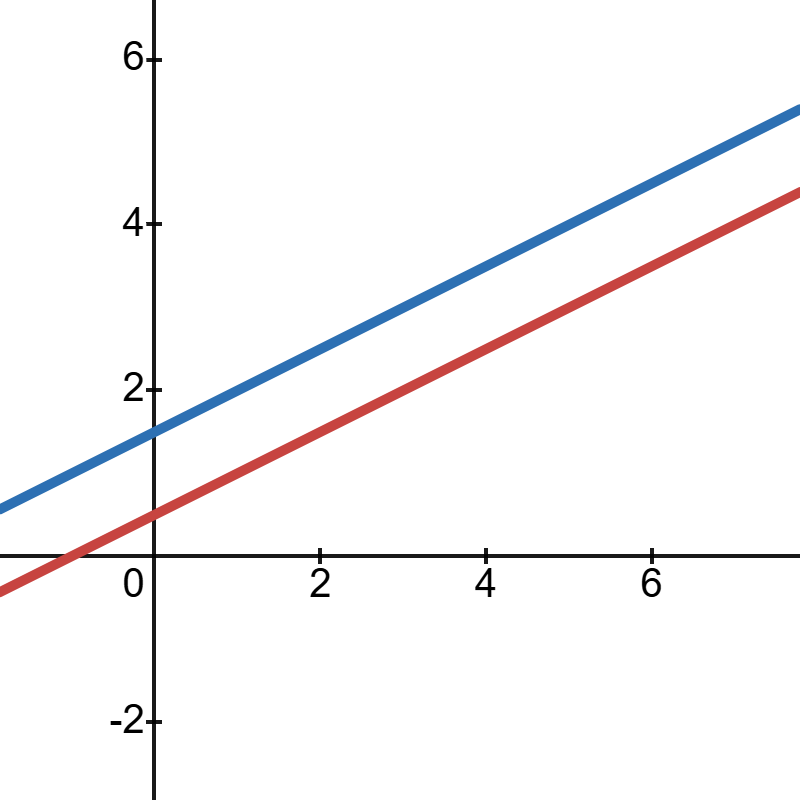
从几何的角度来看,求包含两个变量的两个线性方程组成的线性方程组的解等价于求两条直线的交点。例如:
$$ \begin{align*} x_1 - 2x_2 &= -1 \\ -x_1 + 3x_2 &= 3 \end{align*}$$
这两个方程对应的图形都是直线,数对$(x_1,x_2)$满足这两个方程当且仅当点$(x_1,x_2)$是这两条直线的交点. 容易验证,这个方程组有唯一解$(3,2)$.
当然,两条直线不一定交于一点,它们也可能平行或者重合,分别对应着无解和无穷多解的情况,如下图:
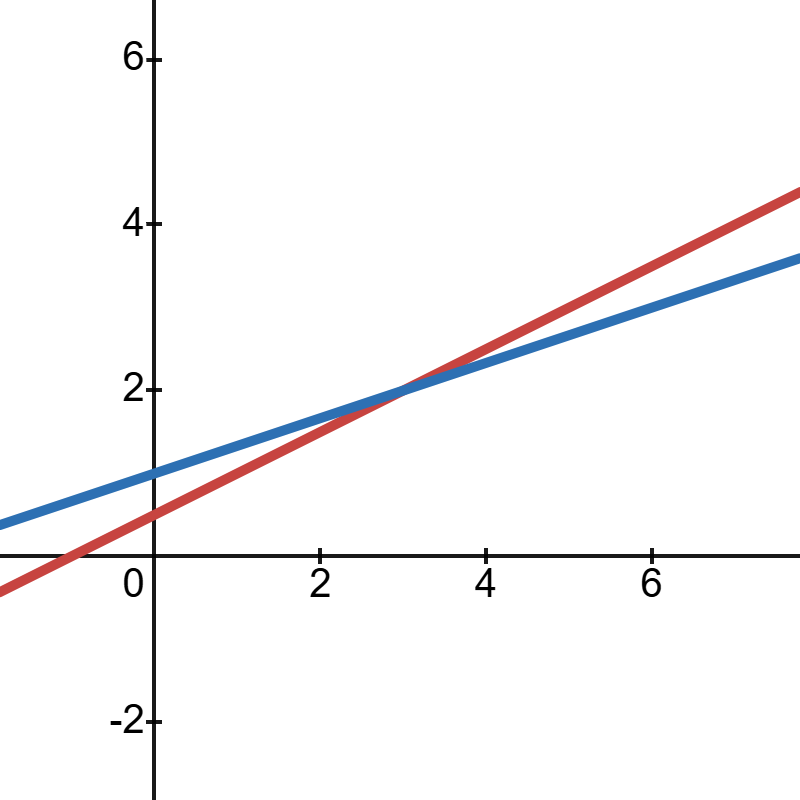

上面三幅图说明了线性方程组的下列基本事实,后面的章节会予以证明.
1.无解.
2.有唯一解.
3.有无穷多解.
如果一个线性方程组有解,我们称它是相容的;若它无解,我们称它是不相容的.
矩阵记号
为了方便研究线性方程组,我们把一个线性方程组包含的主要信息用一个紧凑的矩形阵列表示,称为矩阵. 给出方程组
$$ \begin{align*} x_1 - 2x_2 + \quad x_3 &= 0 \\ 2x_2 - 8x_3 &= 8 \\ 5x_1 \quad \quad\quad- 5x_3 &= 10 \end{align*}$$
把每个变量的系数写在对齐的一列中,得到矩阵
$$ \begin{bmatrix} 1 & -2 & 1 \\ 0 & 2 & -8 \\ 5 & 0 & -5 \end{bmatrix}$$
称为方程组的系数矩阵,而添上常数列后得到矩阵
$$ \begin{bmatrix} 1 & -2 & 1 &0 \\ 0 & 2 & -8 &8\\ 5 & 0 & -5 &10\end{bmatrix}$$
称为它的增广矩阵.
向量与向量方程
也可以从向量的角度理解。我们将中学的向量概念拓展如下:
$$ 若n是正整数,则\mathbb{R}^n表示所有n个实数数列的集合,通常写成n\times1列矩阵的形式,如$$
$$\mathbf{u} = \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix}$$
$\mathbb{R}^n$中向量的性质类似于二维向量$\mathbb{R}^n$的性质,我们将在后面的章节详细展开.
以上面的方程组为例,要从向量的角度理解
$$ \begin{align*} x_1 - 2x_2 + \quad x_3 &= 0 \\ 2x_2 - 8x_3 &= 8 \\ 5x_1 \quad \quad\quad- 5x_3 &= 10 \end{align*}$$
可以写成
$$x_1\begin{bmatrix} 1 \\ 0 \\ 5 \end{bmatrix}+x_2\begin{bmatrix} -2 \\ 5 \\ 6 \end{bmatrix}+x_3\begin{bmatrix} 1 \\ -8 \\ -5 \end{bmatrix}=\begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$$
即:找到一组数,将$\begin{bmatrix} 7 \\ 4 \\ -3 \end{bmatrix}$表示为$\begin{bmatrix} 1 \\ 0 \\ 5 \end{bmatrix}\begin{bmatrix} -2 \\ 5 \\ 6 \end{bmatrix}\begin{bmatrix} 1 \\ -8 \\ -5 \end{bmatrix}$的线性组合.
线性代数的一个主要思想就是研究可以表示为某一向量集合的线性组合的所有向量. 严谨定义如下
若 $v_1, v_2, \dots, v_p$ 是 $\mathbb{R}^n$ 中的向量,则 $v_1, v_2, \dots, v_p$ 的所有线性组合所成的集合用记号$\text{Span}\{v_1, v_2, \dots, v_p\}$ 表示,称为由 $v_1, v_2, \dots, v_p$ 所生成(或张成)的 $\mathbb{R}^n$ 的子集。也就是说,$\text{Span}\{v_1, v_2, \dots, v_p\}$ 是所有形如$c_1v_1 + c_2v_2 + \dots + c_pv_p
$的向量的集合,其中 $c_1, c_2, \dots, c_p$ 为标量。
这样,判断线性方程组解的情况的问题就转化为了判断常数向量和矩阵的列向量张成的空间的关系问题. 即:
1.无解-->向量不在张成的空间内.
2.有唯一解-->向量在张成的空间内.
3.有无穷多解-->向量在张成的空间内.
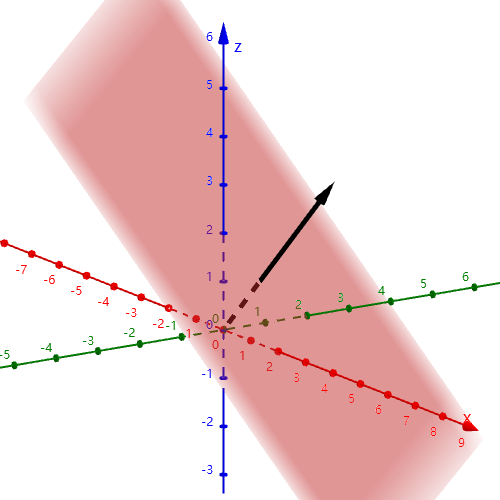
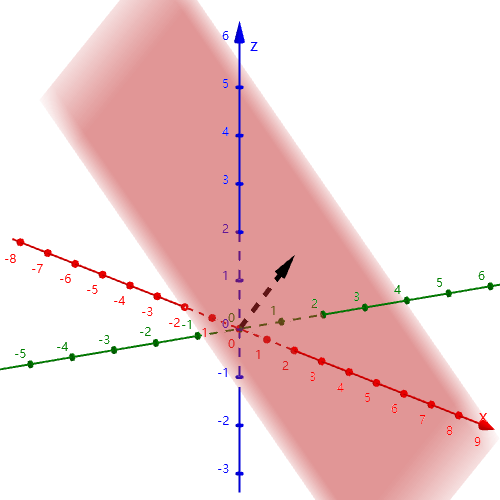
如何区分有唯一解和有无穷多解?如何解出对应的解?接下来的章节将解答这些问题.